Understanding Buyer Premium
©True Blue Auctions
Hiring the right auctioneer or company will make a big difference in the total revenue that a seller or consignor receives. By understanding the factors that contribute to the final revenue, it is possible to narrow down the choices and select an auction company that will provide the largest revenues for the sale of an item.
Methods of Charging
The method that an auctioneer or an auction company uses to charge for their services will impact the final revenue that is generated by the auction. An auctioneer can use two methods of charging: buyer premiums or a sales commission.
Dr. Jonathan Wu’s research report states that buyer premiums were first introduced at Christie’s, the famous art auction house, in 1975. Instead of charging the seller, the buyer premium is added to the sales price of the purchase. Buyers are paying the charge in addition to the price they offered for the item.
Buyer premiums are not the same as a sales commission. A sales commission is paid by the seller to the auctioneer or company from the revenues that are generated. For example, if an auctioneer has a sales commission of 10 percent and a product sells for $1,000, then the seller pays $100 to the auctioneer, resulting in revenue of $900.
Although the two basic types of charges are buyer premiums and sales commissions, some auctioneers will use a combination of both charges, such as a 5 percent sales commission and a 5 percent buyer premium.
Using Buyer Premium to Obtain Larger Revenue
Although buyer premiums and sales commissions may seem to offer similar revenues, the reality is that buyer premiums will result in larger revenue for the seller or consignor.
Dr. Jonathan Wu’s reports in his research for the National Property Management Association that every 1 percent of a sales commission will actually reduce the total revenue potential by more than 1 percent when compared to a buyer premium. As a result, the total revenue generated by a sale will reduce as the sales commission increases when compared to a buyer premium with the same percentage.
For example, let’s say seller one hired an auction company that charges a 10 percent sales commission and no buyer premium. If the revenue from the sale is $20,000, then the seller will receive $18,000.
Assume that seller two hired an auction company that charges a 10 percent buyer premium and no sales commission. With the same bid of $20,000, the buyer will pay $22,000 and the seller will receive the full $20,000.
Dr. Jonathan Wu states that the Sales Commission Equivalent is equal to the buyer premium divided by one plus the buyer premium. For example, a buyer premium of 10 percent would result in a formula of 0.10/(1+0.10) or 0.10/1.1, which equals 0.091, or 9.1 percent.
Although 10 percent is the stated charge for both auctioneers, the actual revenue that the seller receives when the auctioneer uses a buyer premium is almost 1 percent more than the revenue from an auctioneer who charges a sales commission.
The higher the percentage charged for auctioneer services, the greater the difference in revenue amounts becomes. For example, if the charges were 20 percent, then the actual cost of the buyer premium is roughly 16.67 percent instead of 20 percent. As a result, the seller will receive roughly 3.3 percent more when a buyer premium is charged.
Although it is true that an auctioneer who charges a buyer premium will provide top-dollar during an auction, it is important to consider the impact of human behavior. A hammer price, which suggests that the buyer will bid an
equivalent sales price for an item, overlooks possible variations in how buyers might calculate their maximum bid.
A hammer price does not always apply to the situation. If seller two hires an auctioneer who charges a 10 percent buyer premium and the buyer adds the premium into the total cost, then the buyer may bid lower.
The revised calculation to account for a buyer estimating the cost with a buyer premium means:
• Seller 1 pays a net seller commission of 10.00% [(1,000 – 100)/1,000] or a total revenue of $900
• Seller 2 pays a net seller commission of 9.10% [(1,000 – 909.09)/1,000] or a total revenue of 909.09
On the other hand, buyers can also miscalculate the proceeds by estimating according to the 10 percent rather than 9.1 percent in charges. If the buyer calculates according to the stated percentage, then the calculation would
revise further.
• Seller 1 pays a net seller commission of 10.00% [(1,000 – 100)/1,000] or a total revenue of $900
• Seller 3 pays a net seller commission of 9.10% [(990 – 900)/990] or a total revenue of $900
Since the third buyer is calculating based on adding 10 percent to the sale price, the buyer might bid $900 as the hammer price. Dr. Wu’s calculation estimates that the buyer will pay 900 x 1.1, or $990 when the buyer premium is calculated incorrectly.
Seller
Seller One
Seller Two
Seller Three
Method Of Charging
10% sales commission
10% buyer premium with
accurate buyer calculations
10% buyer premium with
inaccurate buyer calculations
Total Revenue On $1,000 Item
$900
$909.09
$900
Total Auctioneer Income
$100
$91.91
$90
even when a buyer does not overlook the additional cost that is added to a bid.
Sellers should normalize sales commissions and buyer premiums using the Equivalency Formula when evaluating auctioneers based on price.
Two formulas have been derived that can convert the buyer premium into its sales commission equivalent (and vice versa) in terms of its effect on the
seller’s revenue. We call these the Equivalency Formulas.
Sales Commission Equivalent = [ Buyer Premium / (1 + Buyer Premium) ]
Buyer Premium Equivalent = [ Sales Commission / (1 – Sales Commission) ]
Conversion Table
The tables below convert between buyer premiums and sales commissions while keeping the seller’s revenue constant. See Table Reference: Table 1
| BUYER PREMIMUM .....> Sales Commission | ||
|---|---|---|
| BUYER PREMIMUM | Sales Commission | Gap |
| 1.00% | 0.99% | 0.01% |
| 2.00% | 1.95% | 0.4% |
| 3.00% | 2.91% | 0.09% |
| 4.00% | 3.85% | 0.15% |
| 5.00% | 4.76% | 0.24% |
| 6.00% | 5.66% | 0.34% |
| 7.00% | 6.54% | 0.46% |
| 8.00% | 7.41% | 0.59% |
| 9.00% | 8.26% | 0.74% |
| 10.00% | 9.09% | 0.91% |
| 11.00% | 9.91% | 1.09% |
| 12.00% | 10.71% | 1.29% |
| 13.00% | 11.50% | 1.50% |
| 14.00% | 12.28% | 1.72% |
| 15.00% | 13.04% | 1.96% |
| 16.00% | 13.79% | 2.21% |
| 17.00% | 14.53% | 2.47% |
| 18.00% | 15.25% | 2.75% |
| 19.00% | 15.97% | 3.03% |
| 20.00% | 16.67% | 3.33% |
| 21.00% | 17.36% | 3.64% |
| 22.00% | 18.03% | 3.97% |
| 23.00% | 18.70% | 4.30% |
| 24.00% | 19.35% | 4.65% |
| 25.00% | 20.00% | 5.00% |
| Sales Commission.....> BUYER PREMIMUM | ||
|---|---|---|
| Sales Commission | BUYER PREMIMUM | Gap |
| 1.00% | 1.01% | (0.01%) |
| 2.00% | 2.04% | (0.4%) |
| 3.00% | 3.09% | (0.09%) |
| 4.00% | 4.17% | (0.17%) |
| 5.00% | 5.26% | (0.26%) |
| 6.00% | 6.38% | (0.38%) |
| 7.00% | 7.53% | (0.53%) |
| 8.00% | 8.70% | (0.70%) |
| 9.00% | 9.89% | (0.89%) |
| 10.00% | 11.11% | (1.11%) |
| 11.00% | 12.36% | (1.36%) |
| 12.00% | 13.64% | (1.64%) |
| 13.00% | 14.94% | (1.94%) |
| 14.00% | 16.28% | (2.28%) |
| 15.00% | 17.65% | (2.65%) |
| 16.00% | 19.05% | (3.05%) |
| 17.00% | 20.48% | (3.48%) |
| 18.00% | 21.95% | (3.95%) |
| 19.00% | 23.46% | (4.46%) |
| 20.00% | 25.00% | (5.00%) |
| 21.00% | 26.58% | (5.58%) |
| 22.00% | 28.21% | (6.21%) |
| 23.00% | 29.87% | (6.87%) |
| 24.00% | 31.58% | (7.58%) |
| 25.00% | 33.33% | (8.33%) |
The graph below illustrates that as the sales commission increases, the gap increases between it and the buyer premium whichgenerates an equivalent
seller revenue. (See Figure 1)
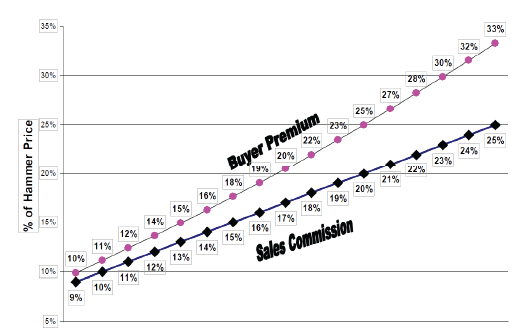
Figure 1. Graph of Percent of Hammer Price with Buyer Premium and Sales Commission, “Sales Commissions & Buyer Premiums” by Dr.Jonathan K.Wu
The following is the algebraic proof for the Equivalency Formulas.
Definitions
Let V = $ value of the asset to the buyer (final auction price plus buyer premium)
Let P = $ final auction sale price of the asset (excluding the buyer premium)
Let s = % sales commission
Let b = % buyer premium
Let RS = $ revenue to the seller
Relationship A: Value of Asset to the Buyer vs. Final Auction Sale Price
The value of the asset to the buyer (V) is equal to the final auction sale price of the asset (P) plus the buyer premium paid by the buyer (b x P). But how do we express the final auction sale price (P) as a function of the value of the asset to the buyer (V) and the buyer premium (b)? (See Equation 1)
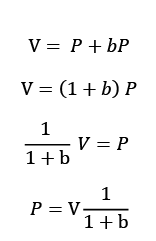
Equation 1. Value to Buyer vs. Final Sale Price, “Sales Commissions & Buyer Premiums” by Dr.Jonathan K.Wu
Relationship B: Seller’s Revenue vs. Value of Asset to the Buyer
The seller’s revenue from the auction (RS) is equal to the final auction sale price (P) minus the sales commission paid by the seller (s x P). How do we
express the seller’s revenue (RS) as a function of the buyer premium (b), sales commission (s) and value of the asset to the buyer (V)? (See Equation2)

Equation 2. Seller Revenue vs. Value of Asset Buyer, “Sales Commissions & Buyer Premiums” by Dr.Jonathan K.Wu
How do express the sales commission (s) as a function of the buyer premium (b), or vice versa, if we set the seller’s revenue (RS) to be equivalent in either case?
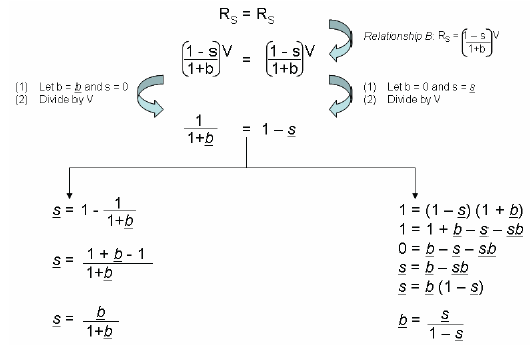
Equation 3. Sales Commission vs. Buyer Premium, “Sales Commissions & Buyer Premiums” by Dr.Jonathan K.Wu

